С.Б.КРЫЛОВ, канд. техн. наук (НИИЖБ), Исследование решения уравнений изгиба железобетонных плит с трещинами
Существует несколько теории расчета железобетонных плит и тонких пластинок с трещинами. Пожалуй, наиболее детально деформирование таких конструкций описывается теорией, основы которой были разработаны Н.И. Карпенко и которая успешно развивается его школой.
В соответствии с этой теорией [1] напряженно- деформированное состояние железобетонной пластинки с трещинами описывается системой геометрических уравнений, физических уравнений и уравнении равновесия. При строгом подходе эта система сводится к результирующей системе нелинейных дифференциальных уравнений в частных производных (так как в нее входят жесткостные коэффициенты, являющиеся функциями перемещений). Наиболее распространенным способом решения такого рода задач является расчет с использованием пошагового нагружения, считая значения жесткостных параметров известными, с последующим уточнением их значений в различных точках рассчитываемой конструкции на каждом шаге нагружения. Такой подход позволяет рассматривать жесткостные параметры не как функции от перемещений, а как функции от координат х и у.
Попытка свести систему из трех видов уравнений к результирующей системе дифференциальных уравнений связана с довольно сложными выкладками. Поэтому часто используют упрощающие допущения. Это в большинстве случаев приводит к значительным изменениям в строении получаемой системы уравнений по сравнению с истинной. Ниже приводятся результаты строгого вывода системы дифференциальных уравнений в рамках указанного выше подхода.
С учетом геометрических уравнений [1], силы и моменты выражаются через перемещения U.V.W точек срединной плоскости пластинки при помощи следующих дифференциальных зависимостей:

Дифференциальные уравнения изгиба пластинки получаются путем подстановки выражений (1) в уравнения равновесия [1|. После преобразований получаем:

Приближенное общее решение будем разыскивать в виде суммы частного решения неоднородной системы (2) и приближенного общего решения соответствующей однородной системы. Частное решение можно принять в виде:
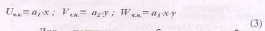
Для получения приближенного общего
решения высокой точности, желательно использовать в качестве аппроксимирующих функций точные
фундаментальные решения однородной системы, соответствующей уравнениям (2). В связи с этим была исследована возможность построения
фундаментальных решений в полиномах. Приближенное решение принималось в виде многочленов десятого порядка:
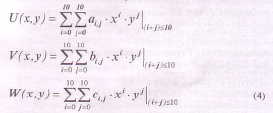
При этом ставились две задачи исследования. Первая задача - установить, будет ли получаемая в результате разрешающая система линейных алгебраических уравнений иметь решение (будет ли она совместна и будет ли достаточно хорошо обусловлена). Вторая задача - установить, сколько разрешающих уравнений будет получено из условия удовлетворения предполагаемым решением уравнений системы (2) и сколькими уравнениями можно дополнить разрешающую систему (чтобы выполнить условия сопряжений с соседними элементами).
Выражения (3) и (4) подставлялись в уравнения (2). После этого приравнивались члены, содержащие переменные х и у в одинаковых степенях. На практике все функции описывались при помощи числовых массивов. Так, каждая из функций (4) описывалась двумерным массивом. Число строк в массиве было равно числу слагаемых в каждом из многочленов (4). Все неопределенные коэффициенты я,у, Ьц , Сц были пронумерованы по порядку. В первом столбце содержались номера неопределенных коэффициентов. Во втором и третьем столбцах — показатели степеней соответственно х и у. После выполнения дифференцирования добавлялся еще один столбец, в котором содержались множители, появляющиеся при дифференцировании отдельных слагаемых многочлена. Таким образом, все операции дифференцирования многочленов, сложения многочленов, умножения их на постоянную величину, сводились к изменению содержания столбцов массивов и к арифметическим операциям между массивами. Такая операция, как формирование системы разрешающих уравнений путем приравнивания членов, содержат одинаковых степенях, также сводилась к компьютерной обработке описанных выше числовых массивов.
Приведем цифровые данные, характеризующие исследованную задачу. Построенные многочлены (4) содержали по 66 членов каждый. После подстановки их в систему уравнений (2) получалась разрешающая система из 165 линейных алгебраических уравнений относительно 198 неизвестных коэффициентов многочленов (4) То есть, система была не полна. Общее чисто свободных неизвестных в ней составило 33.
Дополнительные 33 уравнения должны быть получены из условий сопряжений с соседними элементами или с функциями, выражающими граничные условия, если данный элемент находится на краю пластинки ( с учетом частного решения (3)).
В том случае, если учитываются только поперечные перемещения пластинки W(x,y), то число дополнительных уравнений для каждого элемента составляет 11 штук.
Для исследования вопроса о том, позволит ли разрешающая система уравнений получить решение задачи после дополнения ее или после включения ее в состав более общей системы, был использован следующий подход. Разрешающая система чисто формально дополнялась до полной системы уравнений. Затем значениям коэффициентов в уравнениях (2) присваивались случайные значения, для чего использовался генератор случайных чисел программы “Mathcad 6 PLUS”. При этих значениях вычислялись коэффициенты матрицы левых частей указанной системы. После этого таким же способом задавались случайные значения коэффициентов дополнительных уравнений и их правых частей. Затем, полученная линейная система алгебраических уравнений решалась. Результаты многочисленных испытаний с использованием различных последовательностей случайных чисел показывают, что полученная система уравнений является совместной и позволяет получать решения. Следовательно, система дифференциальных уравнений изгиба железобетонной пластинки с трещинами для общего случая армирования и схемы трещин (2) допускает решения в виде многочленов.
Таким образом, полная система уравнений изгиба железобетонной пластинки с трещинами (физических и геометрических уравнений, а также уравнений равновесия) сведена к системе дифференциальных уравнений с учетом переменных значений жесткостных коэффициентов.
Построено частное решение этой неоднородной системы уравнений изгиба.
Исследованы особенности построения фундаментальных решений соответствующей однородной системы уравнений в виде многочленов. Установлено, что при использовании многочленов удается построить точные фундаментальные решения данной системы.
Бетон и железобетон, 2002 №4