А.И.ПОПЕСКО, д-р техн. наук, проф. (ОООШФ АЛЬТЕРНАТИВА”); О.И.АНЦЫГИН, канд. техн. наук (ГОУВПО “СПбГАСУ”); А.А.ДАИЛОВ, канд. техн. наук (26 ЦНИИ Минобороны России), Численный расчет железобетонных стержней при коррозионных воздействиях
При разработке проектов по реконструкции, а также при возобновлении работ на объектах, строительство или реконструкция которых были прекращены несколько лет назад, необходимо тщательно учитывать техническое состояние конструкций, находившихся в эксплуатации. Практика обследований показывает, что одной из основных причин снижения несущей способности железобетонных конструкций является влияние агрессивных воздействий окружающей среды. Наиболее неблагоприятным результатом такого воздействия является химическая коррозия железобетона. В промышленно развитых странах ущерб от коррозии оценивается в 3.. .5% от валового национального дохода, при этом 13... 19% приходится на долю строительных конструкций. В настоящее время влияние химической коррозии на несущую способность железобетонных конструкций при обследовании оценивается ориентировочно. Поверочный расчет железобетонных конструкций нормирован СНиП 2.03.01-84, в которых отсутствуют главы по расчету железобетонных конструкций с учетом влияния химически агрессивных сред на их несущую способность.
В основу разработанного алгоритма расчета положен подход нелинейной теории железобетона Р.С. Санжаровского с использованием феноменологических зависимостей, характеризующих работу железобетона в химически агрессивных средах, предложенных А.И. Попеско, а также подход А.В. Носарева к дискретизации рассчитываемых систем в пространстве и процессов деформирования во времени.
Рассматриваемая конструкция разбивается по длине на ряд участков (блоков-отсеков), на границах которых предполагается наличие тонких, но жестких на изгиб из своей плоскости, диафрагм. Продольными плоскостями каэдый блок-отсек делится на ряд полос, которые, как полагается, работают в тех же условиях, что и при отсутствии разрезов. Арматура представляется самостоятельными полосами, работающими исключительно на растяжение или сжатие и имеющими жесткую связь с бетоном только в районе жестких диафрагм. Деление продольными плоскостями может отсутствовать, и тогда блок-отсек бетона воспринимается как одна единая полоса. В зависимости от выбора расчетной схемы принимается, что полосы бетона и арматуры жестко или шарнирно соединены с диафрагмами. При этом степень неопределимости системы зависит от ее внешней статической или кинематической неопределимости и числа полос, на которые разделены по высоте блоки-отсеки.
Гипотеза плоских сечений вводится только дискретно - считается, что плоскими сохраняются лишь сечения, которые разделяют рассматриваемую конструкцию на отдельные блоки-отсеки (характерные объемы) с длиной I, зависящей от характера эпюр силовых факторов.
Допускается, что рабочая арматура имеет связь с бетоном конструкции лишь в отмеченных плоских сечениях (жестких диафрагм); в пределах отсеков сцепления арматуры с бетоном нет.
Каждый характерный объем делится по высоте горизонтальными плоскостями на слои, заменяемые в расчетной схеме стержнями с площадью, равной площади поперечного сечения слоя; количество продольных стержней в расчетной схеме, заменяющих слои бетона и стержни или группы стержней арматуры, может быть различным в зависимости от требуемой точности расчета.
По высоте рассматриваемого элемента заменяющие стержни могут быть расположены неравномерно: гуще там, где ожидается наибольшее проявление нелинейных эффектов.

Система стержней, имеющая шарнирное соединение с жесткими диафрагмами (см. рисунок), воспринимает только деформации сжатия или растяжения, деформации изгиба не учитываются. Система стержней в рассматриваемом виде не может воспринимать поперечной силы, поэтому в расчетной схеме, предназначенной для раскрытия статической неопределимости с учетом только двух первых членов формулы Мора, рассматриваемую систему параллельных стержней нужно условно дополнить продольной стенкой, работающей только на сдвиг.
Следует подчеркнуть, что расстояние между диафрагмами лучше принимать равным расчетному расстоянию между трещинами первой очереди, так как данную модель можно использовать при расчетах на прочность, трещиностойкость и деформативность, т.е. с единых позиций оценивать предельные и эксплуатационные состояния.
Принимается допущение о существовании границы, разделяющей здоровый и корродирующий бетоны. Влияние агрессивной среды на бетон рассматривается как фактор, изменяющий во времени его деформативные и прочностные свойства. Количественной характеристикой процесса коррозии бетона является глубина его нейтрализации. В случае кратковременного нагружения зависимость между напряжениями и деформациями бетона аппроксимируется полиномом пятой степени.
При описании процесса работы бетона при длительном нагружении используется нелинейное уравнение теории старения И.И.Улицкого. Для учета влияния длительных процессов на напряженно-деформированное состояние конструкции рассматриваемый период времени (t) разбивается на несколько интервалов. В пределах каждого из них считается, что напряженное состояние конструкций не меняется, а соответствующая часть конечной характеристики ползучести ф“, определенной из диаграмм а-е и г-t, реализуется в конце каждого этапа.
Количественной характеристикой коррозии арматуры являются коррозионные потери рабочего диаметра стержня. Физико-механические характеристики стальной арматуры под влиянием агрессивной среды не изменяются. Для описания закона деформирования арматуры с физическим пределом текучести принимается кусочно-линейная зависимость.
Внешнее воздействие в общем случае представляется в виде изгибающего момента Ми нормального усилия N, приложенных в любой точке (лучше - посредине высоты). Понятие центра тяжести сечения не имеет смысла, так как учитываются нелинейные эффекты. Разрушение моделируется с использованием критерия устойчивости в виде равенства вариаций внешних и внутренних моментов, а также условий прочности по ограничению величины предельных деформаций крайнего сжатого волокна здорового бетона и растянутой арматуры. При заданных М и N расчетная схема наиболее просто решается методом перемещений, где в качестве неизвестных Z1 и Z2 приняты соответственно поворот кромок, окаймленных диафрагмами относительно середины их высоты, и линейное смещение этих кромок.
Система канонических уравнений метода перемещений имеет вид:

Представляя исходные данные в виде векторов и матриц и вводя вектор единиц U порядка п, ще п - число стержней в расчетной схеме, все формулы можно представить в матричном виде: а при нахождении из расчета вектора е с использованием диаграмм а-е для бетона и арматуры получить вектор а, т.е. фактическую эпюру напряжений как по высоте бетонного сечения, так и в арматуре.
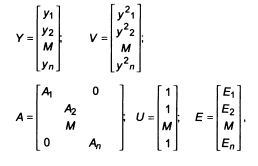
Использование матричного аппарата предполагает определение на каждом этапе векторов М и N. Вектор М включает изгибающие моменты, зафиксированные на стадии упругого расчета и изменяющиеся под действием ползучести и коррозионных воздействий только в полосах бетона последовательной цепи блоков- отсеков, а вектор N - как в бетоне, так и в арматуре. При этом в случае шарнирной связи полос с диафрагмами в блоке-отсеке матричная запись формул для определения М и N претерпит некоторую трансформацию, но суть ее остается той же. Учет влияния ползучести в рассматриваемом интервале времени сводится к реализации дополнительных усилий. Соответствующая часть конечной характеристики ползучести вводится в матрицы релаксаций (или в матрицы податливости, если расчет ведется методом сил).
Стержни, деформации которых на каком-либо этапе приближения превышают предельные, из рассмотрения не исключаются, но их модуль деформации принимается весьма малым. Таким образом, влияние такого стержня на напряженно-деформированное состояние бесконечно мало, но в то же время он присутствует в расчете; это необходимо, так как в процессе последовательных приближений легко можно потерять разорвавшийся стержень из рассмотрения, хотя на последующих этапах, сохрани его, деформации в нем могут и уменьшиться.
Для растянутых или сжатых (от нагрузки или усилий предварительного обжатия) стержней бетона и арматуры необходимо обращаться к своим диаграммам а-е растяжения или сжатия.
В случае наличия преднапряжения необходимо произвести расчет на усилия предварительного обжатия (т0,0о), а при дополнительном нагружении внешней нагрузкой учитывать изменяющуюся степень влияния преднапряжения на прочность элемента в целом в зависимости от стадии работы составляющих материалов: упругой, упруго-пластической и пластической (предельной).
Данный алгоритм позволяет учитывать линейную и нелинейную ползучесть, сравнительно просто определять потери преднапряжения в арматуре от ползучести и усадки, а также теоретически устанавливать для конструкции равновесное напряженно-деформированное состояние.
В соответствии с вышеописанным алгоритмом расчета создана и реализована программа для ЭВМ, позволяющая полностью автоматизировать расчет и оценку напряженно-деформированного состояния железобетонных стержневых конструкций при работе их в условиях коррозионных воздействий (Свидетельство РФ об официальной регистрации программ для ЭВМ №2002611131).
Бетон и железобетон, 2007 №3