С. Б. КРЫЛОВ, д-р техн. наук, П.Д. АРЛЕНИНОВ, инж., НОВАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ
В настоящее время наблюдается повышенный интерес к вопросам устойчивости железобетонных конструкций. Он особенно возрос после аварии оболочечного покрытия аквапарка в Ясенево. Несмотря на то, что эти вопросы изучены достаточно хорошо, в настоящее время в данной области господствует представление об устойчивости железобетонных конструкций, близкое к таковой упругих систем. Это затрудняет исследование работы конструкций и не позволяет выявить некоторые важные особенности их поведения.
Рассмотрим существующие постановки задачи устойчивости и их применимость к железобетонным стержневым элементам.
Эйлерова или бифуркационная постановка задачи
В данной постановке задачи предполагается, что при некотором критическом значении сжимающей силы у центрально-сжатого стержня наряду с прямолинейной формой равновесия появляется изогнутая форма равновесия. Последняя при критическом значении сжимающей силы сколь угодно мало отличается от прямолинейной. Переход от прямолинейной формы к криволинейной осуществляется при действии малого возмущения. При этом предполагается, что прямолинейная форма становится неустойчива, а искривленная - устойчива, т. е. под действием возмущения стержень изогнется и останется в искривленном состоянии.
К железобетонному стержню такая постановка применима не во всех случаях. Это связано с тем, что деформации ползучести, возникающие под действием возмущения, частично необратимы. Поэтому искривленное состояние стержня не всегда свидетельствует о потере устойчивости.
Энергетическая постановка задачи
В данной постановке предполагается, что при некотором значении сжимающей силы прямолинейная форма стержня становится неустойчивой. Устойчивость прямолинейной формы проверяется путем задания возмущения и изучение изменения энергии стержня при переходе его в возмущенное состояние.
Непосредственно такая постановка применима к железобетонным стержневым конструкциям не во всех случаях. Для проявления ползучести бетона возмущение должно быть длительным. Энергия всей деформированной системы будет изменяться во времени. Причем, если потеря устойчивости происходит не мгновенно и растягивается во времени, то, очевидно, для данного мгновения всегда можно подобрать такой прогиб и историю перехода к нему (с мгновенным приращением в конце), чтобы приращение энергии системы в изогнутом состоянии было положительным. Иначе говоря, оценка устойчивости системы зависит еще и от истории возмущения, что потребует дополнительных исследований.
Эйлерова постановка задачи, но с использованием модуля упругости для длительных нагрузок
Данная постановка задачи имеет существенный недостаток, связанный с тем, что, строго говоря, величина принимаемого модуля упругости зависит от истории деформирования и поэтому в общем случае является неопределенной. Кроме того, такой подход, по сути, предполагает потерю устойчивости мгновенную, что скрывает истинное поведение конструкции.
К данному подходу близок подход с использованием интегрального модуля.
Постановка задачи устойчивости типа Ляпунова
Ляпуновым было сформулировано понятие устойчивости движения и понятие устойчивости решения дифференциальных уравнений в символах 8-5. Такой подход применяется и к упругим системам. Система является устойчивой, если для любого сколь угодно малого приращения прогиба 6 можно отметить соответствующее приращение нагрузок е. Тем самым указывается на функциональную зависимость прогиба от нагрузки. При нарушении такого однозначного соответствия, при возникновении неопределенности прогиба при данной нагрузке, наступает потеря устойчивости. Непосредственное использование такого подхода к железобетонным стержневым конструкциям также не всегда возможно. Так, если потеря устойчивости выражается в непрекращающемся возрастании прогиба, то (как было отмечено для энергетического подхода) результат будет зависеть от развития возмущения § во времени. И для оценки устойчивости потребуется дополнительное исследование.
Предлагаемая постановка задачи устойчивости
Все рассмотренные постановки задачи устойчивости имеют дело с различными сторонами этого явления, но при этом не рассматривается сама физическая причина потери устойчивости. С точки зрения механики, явление потери устойчивости стержневой конструкции развивается следующим образом.
При приложении к сжатому стержню поперечного возмущающего воздействия он искривляется. При этом в некотором сечении внешние усилия дают изгибающий момент, складывающийся из произведения продольной силы на перемещение, момента от возмущающего поперечного воздействия и моментов от реактивных усилий. В этом же сечении возникает момент от системы внутренних напряжений, который стремится уравновесить момент от внешних усилий. В устойчивом состоянии при удалении возмущающего воздействия момент внутренних сил оказывается больше момента внешних сил, и стержень стремится к исходному положению.
Момент внутренних усилий зависит от кривизны стержня в данном сечении. При неизменных внешних усилиях и момента от них и при увеличении длины стержня кривизна и внутренний момент будут уменьшаться. В конце концов при некоторой длине внутренний момент будет не в состоянии уравновесить внешний момент. При удалении возмущающего воздействия стержень уже не стремится к исходному положению, что и является потерей устойчивости.
Подобное же явление наблюдается, если рассматривать рост сжимающей силы при неизменной длине стержня.
Поэтому для оценки устойчивости предлагается рассматривать возможность уравновешивания внешних усилий в некотором сечении системой внутренних усилий. Если в изогнутом состоянии, вызванном возмущением, внутренний момент меньше момента от внешних усилий, то стержень является неустойчивым.
Все рассмотренные ранее постановки задачи устойчивости не противоречат друг другу. Также нет взаимных противоречий между ними и предлагаемой постановкой. Например, при расчете упругой стержневой системы методом перемещений потеря устойчивости сопровождается обращением в ноль или сменой знаков членов матрицы единичных реактивных усилий, стоящих на главной диагонали. Это свидетельствует или о точном равенстве моментов внешних и внутренних сил, или о невозможности уравновешивания усилий в элементарном стержне при единичном перемещении конца из-за исчезновения или соответствующей смены направления реактивного усилия. Подобный смысл имеют изменения в матрице коэффициентов левых частей системы уравнений при расчете методом конечных элементов. В этом же причина уменьшения энергии системы в возмущенном состоянии, по сравнению с исходным при потере устойчивости. Это же выражает приравнивание к нулю правой части уравнения изгиба стержня в Эйлеровой постановке.
В то же время предлагаемая постановка задачи предоставляет преимущество при исследовании устойчивости железобетонных стержневых систем. Она заключается в том, что данный подход позволяет ясно увидеть влияние ползучести или релаксации напряжений на устойчивость стержневой системы и проследить ожидаемое поведение конструкции при потере устойчивости. Кроме того, данный подход дает полное основание выполнить те математические действия с уравнением изгиба, которые являются обычными для упругого стержня, но выглядят не достаточно обоснованными для упруго-ползучего стержня.
Описание потери устойчивости упруго-ползучего стержня на основе предлагаемого подхода
Предлагаемая постановка задачи позволяет выявить следующие особенности потери устойчивости центрально-сжатым стержнем из упруго-ползучего материала.
Очевидно, что возможны два вида потери устойчивости. Первый вид - потеря устойчивости с мгновенным искривлением, когда сжимающая сила превышает Эйлерову силу, вычисленную для начального модуля упругости бетона. Второй вид - потеря устойчивости, которая развивается постепенно в течение более или менее продолжительного времени и выражается в безостановочном движении. Причем далеко не всегда это движение будет ускоренное в отличие от подходов, встречающихся в литературе. Поскольку потеря устойчивости растягивается во времени и за это время могут меняться нагрузки, то в отличие от упругой системы, с теоретической и инженерной точек зрения, становится важным вопрос о поведении конструкции в течение заданного времени наблюдения при изменении величины продольной силы и граничных условий Очевидно, что возрастание сжимающей силы вызовет ускорение движения, уменьшение силы - его замедление. При произвольном уменьшении силы, кроме плавного движения, возможны как скачкообразные приращения, так и полное прекращение движения. И, с инженерной точки зрения, будет важным вопрос, как изменятся усилия в сечениях стержня, не произойдет ли его разрушение за время наблюдения. Ответ на эти вопросы с использованием ранее предложенных постановок задачи вызывает серьезные сложности.
Математическая сторона задачи
Математически отмеченные особенности явления потери устойчивости железобетонного стержня могут быть описаны с использованием уравнения изгиба стержня из упруго-ползучего материала, предложенного в НИИЖБе.

В этом уравнении t - время; х - продольная координата оси стержня; v - поперечное перемещение оси стержня; мч - изгибающий момент от поперечных нагрузок; N - сжимающая сила; Е - модуль упругости материала; R - ядро релаксации напряжений для однородного материала, моделирующего железобетон, построенное на основе любой из известных теорий ползучести бетона; А, В, С- постоянные, учитывающие особенности поведения материала (знаки членов уравнения зависят от выбора правила знаков).
Данное уравнение позволяет учесть целый ряд особенностей поведения материала, в том числе трещинообразование. Единственным ограничением является то, что оно относится к участку стержня, на котором все свойства материала можно принять постоянными по х.
В соответствии с предложенным подходом в задаче устойчивости рассмотрим уравнение с правой частью, равной нулю. Отсчет времени (t0) начинаем с того момента, когда стержень был искривлен некоторым возмущающим воздействием. Затем причина, вызвавшая возмущение, была устранена, и далее деформации стержня развиваются свободно (в соответствии только с граничными условиями, продольной силой и особенностями материала).
Тогда функция v(t0,x) будет представлять собой начальное условие, выражающее начальное искривление в результате возмущения. Функция v(f0,.v) здесь рассматривается как известная, удовлетворяющая граничным условиям задачи. В этом проявляется та неопределенность, которая свойственна задачам устойчивости. Для получения не нулевого должно быть = 0 Это позволяет использовать ее в качестве правой части уравнения Уравнение устойчивости при этом примет вид

Тогда для каждого номера к будет получаться свое уравнение вида (6). Т.е. каждая k-я составляющая решения (7) будет изменяться во времени по своему закону. Это вполне соответствует действительности. Так, если создать начальное возмущение стержня по некоторому сложному закону со множеством изгибов, то при свободном деформировании будет происходить и изменение прогиба в среднем, и выравнивание стержня, те. будет меняться и форма, и прогиб.
Полученное решение (7) не является общим, так как не позволяет удовлетворять всем граничным условиям, если они меняются во времени. Это может быть в том случае, если стержень входит в состав стержневой системы (например, как составная часть более длинного стержня при разбиении его на участки с постоянными свойствами, или как часть статически неопределимой системы). Учитывая, что подстановка в уравнение (2) решения в виде ряда Фурье по косинусам приводит к тому же интегральному уравнению (6), а также to, что в уравнение (2) входит производная по х только второго и четвертого порядка, можно записать решение в более общем виде
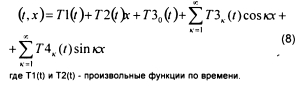
Функции T3K(t) и T4K(t) определяются из решения интегральных уравнений. Поэтому граничные условия в начальный момент времени выполняются за счет задания соответствующих постоянных (в решении вида (7)) в начальный момент времени, а изменение граничных условий во времени учитывается с помощью произвольных функций Т1 (t) и T2(t). (Например, если рассматриваемый стержень входит как составная часть в состав более длинного нелинейного стержня, то Т1 (t) и T2(t) позволяют учесть изменения во времени среднего угла поворота и среднего смещения рассматриваемого элемента). Если форма стержня в ходе деформирования меняется качественно (из-за изменения граничных условий), то задача может быть решена путем разбивки на несколько временных интервалов, в пределах которых изменение граничных условий не является качественным.
Заключение
Таким образом, предложен новый подход к решению задачи устойчивости железобетонного стержневого элемента. Предложенный подход более строго согласуется с действительным поведением стержневых элементов, материал которых обладает ползучестью.
Данная постановка задачи устойчивости (при потере устойчивости, растянутой во времени) и ее решение, в отличие от ранее предложенных, позволяют выделить следующие особенности в поведении конструкции:
1. Форма изгиба стержня из упруго-ползучего материала и величина прогиба при потере устойчивости зависят от начального возмущения.
2. Поведение стержня после превышения силой критического значения, в некоторый момент времени, выражается в движении. Причем закон этого движения связан с историей нагружения стержня продольной нагрузкой.
Бетон и железобетон, 2007 №5